그람-슈미트 정규직교화(Gram-Schmidt Orthonormalization)
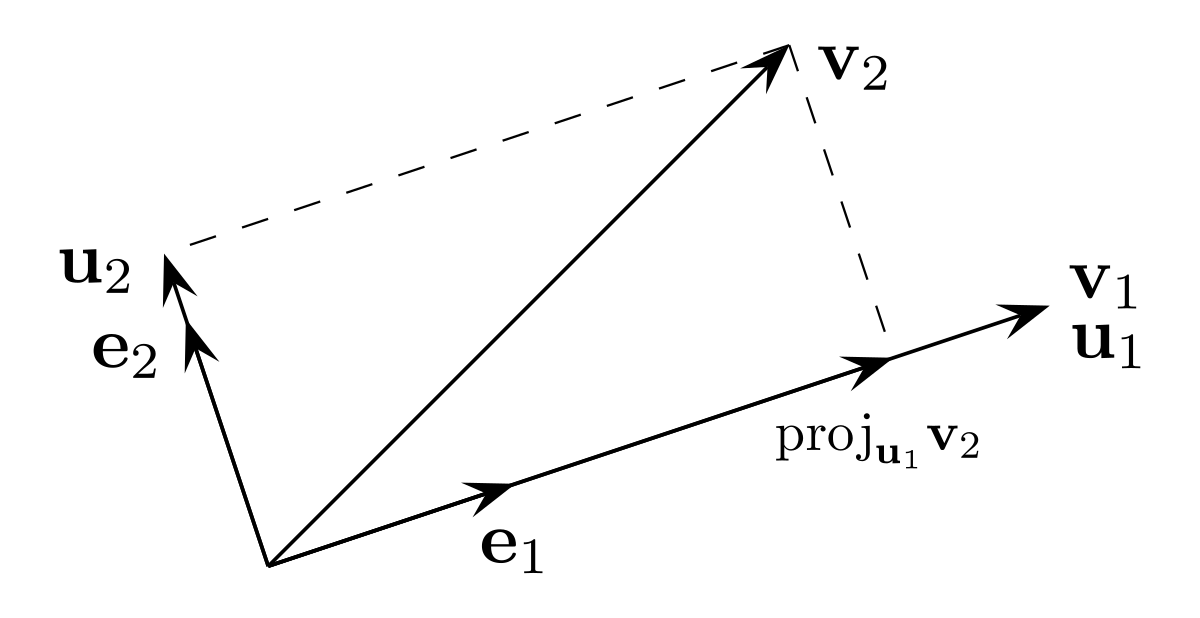
이미지 출처: https://en.wikipedia.org/wiki/Gram–Schmidt_process
📈 그람-슈미트 정규직교화란?
주어진 일차독립 벡터 집합을 서로 직교하고 정규화된 벡터 집합(정규직교기저)으로 변환하는 선형대수 기법.
그람-슈미트 과정은 벡터 공간에서 정규직교 기저(orthonormal basis) 를 구성하는 알고리즘으로, 그래픽스, 물리, AI 계산 등 게임 개발의 다양한 수학적 처리에 사용된다.
📈 그람-슈미트 정규직교화가 필요한 이유
🚫 기존 벡터 집합의 문제점
- 선형 독립이지만 서로 직교하지 않음 → 계산 불편
- 벡터 정규화가 필요하지만 단순 정규화만으론 기저가 아님
- 직교성 + 단위 벡터 → 계산 최적화 및 안정성 확보
✅ 해결책
그람-슈미트 과정은 직교성과 정규화 두 조건을 모두 만족하는 벡터 집합을 만들어 계산 효율을 높인다.
📈 과정 설명
주어진 벡터 집합 $ {v_1, v_2, \dots, v_n} $ 에서 정규직교 기저 $ {u_1, u_2, \dots, u_n} $ 을 구성하는 단계:
- $ u_1 = \dfrac{v_1}{|v_1|} $
- $ u_2’ = v_2 - \mathrm{proj}_{u_1}(v_2), \quad u_2 = \dfrac{u_2’}{|u_2’|} $
- $ u_k’ = v_k - \sum_{j=1}^{k-1} \mathrm{proj}_{u_j}(v_k), \quad u_k = \dfrac{u_k’}{|u_k’|} $
$ \mathrm{proj}_u(v) = \dfrac{\langle v, u \rangle}{\langle u, u \rangle} u $
📈 탄젠트 공간이란?
- 탄젠트 공간(Tangent Space) 은 표면에 붙어 있는 좌표계
- 보통 (Tangent, Bitangent, Normal)의 세 축으로 구성됨
- 노멀맵에 저장된 법선 정보는 이 좌표계 기준으로 되어 있기 때문에, 이를 월드 공간으로 변환하려면 TBN이 필요함
📈 그람-슈미트와 탄젠트 공간(TBN)의 관계
셰이더에서 탄젠트 공간(Tangent Space)을 구성할 때 사용하는 수학적 원리는 바로 ‘그람-슈미트 정규직교화’이다!
우리가 흔히 HLSL 또는 GLSL에서 Normal Mapping을 구현할 때 사용하는 TBN 행렬(Tangent, Bitangent, Normal)은 단순한 벡터 집합이 아니라 정규직교기저(Orthonormal Basis)다. 그리고 이 기저는 종종 그람-슈미트 정규직교화(Gram-Schmidt) 과정에 의해 만들어진다.
📈 DirectX HLSL 예제
void NormalMapping(float2 uv, float3 normal, float3 tangent, SamplerState samp)
{
float4 map = MaterialMaps[MATERIAL_TEXTURE_NORMAL].Sample(samp, uv);
//Material.Diffuse = map;
[flatten]
if (any(map.rgb) == false)
return;
float3 coord = map.rgb * 2.0f - 1.0f; //-1.0f ~ +1.0f
//임의로 공간 만들기(탄젠트 공간) - 축 변환
float3 N = normalize(normal); //Z
float3 T = normalize(tangent - dot(tangent, N) * N); //X
float3 B = cross(N, T); //Y
float3x3 TBN = float3x3(T, B, N);
coord = mul(coord, TBN);
//Material.Diffuse = map;
Material.Diffuse *= saturate(dot(-LightDirection, coord));
}
📈 이 코드에서 일어나는 정규직교화
| 단계 | 의미 | 그람-슈미트 과정과의 연결 |
|---|---|---|
N = normalize(normal) | 단위 법선 벡터 생성 | ( u_1 = \frac{v_1}{|v_1|} ) |
T = normalize(tangent - dot(tangent, N) * N) | Normal에 직교한 벡터 생성 | ( u_2 = \frac{v_2 - \text{proj}_{u_1}(v_2)}{|…|} ) |
B = cross(N, T) | T와 N에 직교한 벡터 생성 | 세 번째 정규직교 벡터 구성 |
즉, 이 TBN 구성 과정은 실제로는 그람-슈미트 정규직교화를 최소 2단계 적용한 결과라고 할 수 있음.
📈 TBN = 정규직교기저
- 정규직교기저란: 서로 수직이고 길이가 1인 벡터 집합
- T, B, N은 모두 단위벡터이며 서로 직교 → 정확한 공간 변환 가능
- 이는 그람-슈미트를 통해 정렬되지 않은 벡터 → 정규직교 벡터로 변환한 것과 같음
📈 활용 사례 (게임 개발)
🎮 1. 카메라 회전
- 시야 벡터를 정규직교기저로 구성해 정확한 회전 및 이동 처리 가능
🎮 2. 로컬 좌표계 구성
- 물체의 방향, 앞/옆/위 벡터를 동적으로 정규직교화해 안정적 제어
🎮 3. AI 시야 처리
- 정규직교 기저로 시야 벡터 범위를 계산하거나 상대 위치 추적에 활용
📈 장단점
| 장점 | 단점 |
|---|---|
| 직교성과 정규화를 동시에 만족 | 계산량 증가 (벡터 수가 많을수록 연산량 많아짐) |
| 수학적 안정성과 계산 효율 확보 | 입력 벡터가 선형 독립이 아닐 경우 실패 가능 |
| 그래픽스, 물리, AI에 활용 가능 | 부동소수점 오차로 인해 직교성이 약간 깨질 수 있음 |
📈 최종 정리
TBN 행렬은 Normal Mapping에서 노멀 벡터를 변환하는 데 필요한 직교좌표계이다. 이 TBN을 구성할 때 사용하는 수학적 핵심 원리가 그람-슈미트 정규직교화이다.
Normal 벡터를 기준으로 Tangent를 직교화하고, 둘의 외적으로 Bitangent를 구해 정규직교기저를 완성한다.
이 정교한 구성 덕분에 셰이더의 조명과 노멀맵 결과가 정확하게 계산된다.
출처 :
