벡터의 내적과 외적
↑ 벡터는 점 A와 점 B를 잇는 화살표이다.
📈 들어가기 전…
벡터를 사용하는 이유
GameObject들의 속도, 바람, 저항, 충돌, 위치 판단 등 많은 요소들을 벡터로 표현할 수 있다.
벡터의 내적을 이용해서 오브젝트 위치의 전·후방을 판별할 수 있다. 플레이어의 시선(forward) 중심으로 좌, 우 90도가 넘어가는 순간코사인 값은음수를 갖기 때문에, 플레이어 시선의 벡터와 target의 위치벡터를 내적해서 양수값이면 플레이어의 전방, 음수값이면 플레이어의 후방에 위치한다.벡터의 외적은 보통 오브젝트 위치의 좌우를 판별하는데 사용된다. 플레이어의 시선과 Up 벡터를 중심으로 외적을 구한다면 플레이어의 좌측에 있는 오브젝트는 양수, 플레이어의 오른쪽에 있는 오브젝트는 음수를 반환한다.
📈 벡터란?
벡터는 그리스 수학자인 ‘유클리디안 벡터(Euclidean vector)’의 이름을 따랐으며, 기하학적 벡터(geometric vector)라고도 불린다. 이는 크기와 방향을 모두 가지는 어떤 양으로 정의되며, 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성요소이다. 일반적으로 벡터는
화살표로 표현한다.화살표가 가리키는 쪽은방향을 나타내며화살표의 길이는크기를 나타낸다.
📈 벡터의 내적(內積; inner product)
<img src=/assets/img/blog/math/vector_inner_product.png" style="width: 832px; height: auto;" >
내적은 벡터를 곱하는 개념 중 하나인데, 이는 ‘쌓을 적(積)’이라는 한자로 표현된다. 이는 두 벡터의 방향이 일치하는 정도에 따라서 곱을 한다. 예를 들어, 두 벡터의 방향이 완전히 일치하면 각 벡터의 크기를 그냥 곱하고, 두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 곱이 0이 된다. 즉 내적은 하나의 벡터를 다른 벡터로 * 정사영 시켜서 그 벡터의 크기를 곱하는 것으로 이해할 수 있다.

내적의 값을 구하는 수식은 두 벡터 사이에 기호로 가운데 점(dot)을 찍는 것( · )이며, 이는 벡터a와 b의 절대값을 곱하고 코사인 세타 값을 곱하면 된다.
* 정사영(Orthogonal Projection) : 한 벡터를 다른 벡터에 수직으로 내린 선상에 있는 점을 찾는 것을 말한다. 즉 정사영은 두 벡터 사이의 각도와 관련이 있으며, 이를 통해 한 벡터를 다른 벡터의 방향으로 투영시키는 것이라 볼 수 있다.
📈 벡터의 외적(外積; outer product)
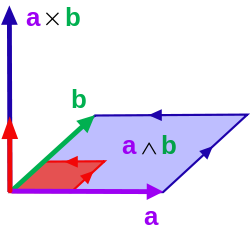
두 벡터를 곱하는 내적 외에 외적도 존재한다. 외적의 결과값은 벡터이며, 이 벡터의 방향은 곱하는 두 벡터에 수직하고 크기는 두 벡터가 이루는 평행사변형의 넓이이다. 내적의 연산 기호는 닷(dot; ·)을 사용하며, 수식은 벡터a와 b의 절대값을 곱하고 코사인 세타 값을 곱하면 된다. 외적의 연산 기호는 크로스(cross; χ )이며, 수식은 각 벡터의 외적의 크기(절대값)를 곱하고 사인 세타 값을 곱하면 된다.
📈 내적과 외적의 차이
수학적으로 접근한다면 내적과 외적은 서로 상관이 없다. 즉 두 가지 형태의 다른 연산이 존재하는 것이라 볼 수 있다. 다만 내적의 결과값은 스칼라이고, 외적의 결과값은 벡터이다.
위에서 서술한 것과 같이 게임 프로그래밍에서 바라보는 벡터의 내적과 외적은 다소 차이가 있다. 내적은 0~180도 사이에서만 구할 수 있기 때문에 전·후방 값만 알 수 있으며, 반대로 외적은 중앙(0)을 기준으로 좌(-1)·우(1) 값을 알 수 있다. 즉 내적과 외적을 함께 쓰게 되면 360도 위치와 방향을 구현할 수 있다. (해당 부분은 다시 정리)
출처 :
- 칸 아카데미 - 벡터란?
- https://wikidocs.net/22384
- https://amirazmi.net/dot-products-in-games-and-their-use-cases/
- https://gnaseel.tistory.com/18#google_vignette
